Category: Networks

Posted on

Attempt at network stress testing in R

I’ve been asked by reviewers to stress test two networks following Jeong &  Barabási (2000). Critically the reviewers asked for an exploration of how network diameter changed as progressively larger numbers of nodes were randomly dropped from the networks.

Although the netboot library makes it trivial to do a case-drop bootstrap on a network, it reports a limited set of network statistics and diameter is not one of them.

Here’s an attempt to run a stress test on network diameter for a small (1000 node) randomly generated ring network. I’m sure there are more efficient ways of doing this, and I’m concerned that the algorithm might struggle with the large real-world networks I’ll be applying it to, but I’m proud of the pretty output for now:

library(pacman)
library(tidyverse)
library(tidygraph)
library(igraph)
library(ggplot2)

#Function graphdropstats accepts graph object and number of cases to drop
#drops ndrop cases(vertices) (using uniform random distribution to identify nodes to drop)
#then returns statistic on subgraph, in this case diameter
# V(graph) gives list of nodes in graph
# vcount(graph) gives number of vertices, but more efficient to get this from length of V(graph)

graphdropstats <- function(graph,ndrop){
 keepnodes<-V(graph) #vector of vertex ID's in graph
 droplist<-sample(as_ids(keepnodes),ndrop)
 keepnodes<-keepnodes[-droplist] #vector of positions in keepnodes to drop
 samplegraph<-induced_subgraph(graph,keepnodes)
 return(diameter(samplegraph))
}

#generate graph for testing
graph1<-create_ring(1000)

## sampling with nreps replications, dropping ndrop nodes at random and saving statistics; 
## and incrementing ndrop each time until ndropstop
nreps=100
ndropstop=100
ndrop=1
allresults<-vector("numeric", nreps)

for (ndrop in 1:ndropstop){
 result<-vector("numeric", nreps)
 for (i in 1:nreps) {
 result[i] <- graphdropstats(graph1,ndrop)
 }
if(ndrop > 1) allresults<-rbind(allresults,result)
}

allresults <- allresults[-1,] #drop first row of matrix which otherwise is blank
#allresults 
matplot(allresults, type='p', pch=15, col=c("gray70"),xlab="N vertices dropped at random", ylab="Network diameter")
index<-1:(ndropstop-1)
lines(index, rowMeans(allresults), col = "red", lwd = 2)

#Edit 27/3/2018: bugfix

This gives us this plot:

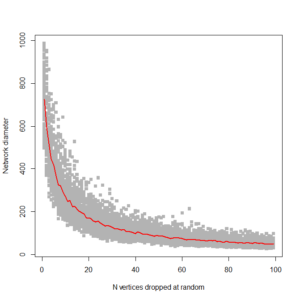
…. which is pretty much what I’m looking for.  It shows, as expected, that ring networks are highly vulnerable to node dropout. Compare to a 1000 node scale-free network:

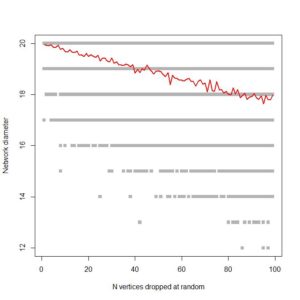
Fingers crossed that it’s efficient enough to run on large co-authorship networks!

 

  • [DOI] Albert, R., Jeong, H., & Barabási, A.. (2000). Error and attack tolerance of complex networks. Nature, 406(6794), 378–382.
    [Bibtex] 
    @article{Jeong2000, title={Error and attack tolerance of complex networks}, volume={406}, url={http://dx.doi.org/10.1038/35019019}, DOI={10.1038/35019019}, number={6794}, journal={Nature}, publisher={Springer Nature}, author={Albert, Réka and Jeong, Hawoong and Barabási, Albert-László}, year={2000}, month={Jul}, pages={378–382}}

 

Posted on

An intriguing computer-based metaphor for culture

Psychologists have exploited computers as metaphors for the human brain ever since their invention. Concepts like “short term memory” and “long term memory” as functional cognitive units that pass information from one to another owe their provenance to computer metaphors.

These metaphors, however, are based on particular technical instantiations of computing; there are unimaginably many ways to instantiate computers as technological objects, including in DNA, slime, and liquid crystal. Even the cloud based systems powering technology experiences today are radically different from the self-contained computing units that spawned the computer-based metaphors at the heart of cognitive psychology. For example,  web-pages hardly ever exist on a single server anymore. When called they are constructed on-the-fly from databases and servers with the illusion of being a unitary object. This very webpage was constructed with 93 calls to four domains; each of those calls would have been served by a server accessing multiple databases in order to fulfill the request. A simple blog page is constructed on-the-fly by literally hundreds of processes hosted on multiple servers.

The information-processing metaphor of the human brain is based on the standalone serial computer; and in practice those barely exist anymore. New forms of computing, like “cloud-computing”, radically disrupt these metaphors.

pingfs (ping file system) is a file storage  system that stores data in the internet itself, as packets bouncing between routers in a network. As a  packet is received it is bounced back as a new packet. No local storage exists beyond that required to read the message, bounce it and instantaneously delete the local copy. The data is “stored” primarily between nodes, not within them; like storing tennis balls by juggling them.

This seems like a far better metaphor for memory than the “short term memory”[RAM]/”long term memory”[Hard-drive] distinction. It captures the social nature of memory, and how individuals primarily remember things they are reminded of.

But as a metaphor for social life and memory it could be improved. What if  nodes in the network selectively bounced packets based on agreement and disagreement? What if packets were subtly changed each time they bounced? This would start to approximate a metaphor for culture, and capture how information is simultaneously transmitted and stored; that the act of transmission is also a mechanism of storage.

This metaphor starts to capture some of the magic of cultural memory; moving the locus of action from the inside of individual brains to the spaces between people, as post-structural theorists have long suggested.  Culture, according to this metaphor, is produced and maintained by the constant flurry of interaction between its members. It is what happens between people, not within people, that creates memory.  Obviously, this is only possible if the people have the capacity to “bounce packets” of information in appropriate ways, but it is a metaphor that highlights that meaning and memory cannot be made alone.

 

 

 

 

 

Posted on

Social network structure & collective cooperation

 

In social psychology we’re interested in how group identity and group processes impact on individual experience and behaviour. Until now the field has focused largely on how people perceive groups and identity; and has not worried too much about the structure of social connections. Network structure , however, makes a big difference to social outcomes at collective levels and we’re now getting tools and models to start to make sense of it all.

Allen and colleagues (2017) have recently shown that cooperation is more likely to emerge in networks with fewer but stronger ties at local levels than in networks with more (but weaker) connections. This is theoretically exciting, as it shows that it is possible and fruitful to analyze social psychological constructs in relation to network structure.

It’s also deeply concerning, since the digital platforms that mediate more and more of our social relationships (Twitter; Facebook; Instagram) are cultivating social networks with large numbers of weak ties — exactly the kinds of relationships that, according to Allen et al., will result in less cooperative networks at large scales.

Counterintuitively, if we want more cooperative societies we might need to spend less time on our phones and see fewer people more often.

  • [DOI] Allen, B., Lippner, G., Chen, Y., Fotouhi, B., Momeni, N., Yau, S., & Nowak, M. A.. (2017). Evolutionary dynamics on any population structure. Nature, 544(7649), 227–230.
    [Bibtex] 
    @Article{Allen2017,
author = {Benjamin Allen and Gabor Lippner and Yu-Ting Chen and Babak Fotouhi and Naghmeh Momeni and Shing-Tung Yau and Martin A. Nowak},
title = {Evolutionary dynamics on any population structure},
journal = {Nature},
year = {2017},
volume = {544},
number = {7649},
pages = {227--230},
month = {mar},
doi = {10.1038/nature21723},
file = {:Allen2017 - Evolutionary dynamics on any population structure:},
owner = {MQ},
publisher = {Springer Nature},
timestamp = {2017-09-07},
}